Du er ikke logget ind. Det betyder at dine svar ikke bliver gemt.
Godt. Den formel vi nu har lært gælder, men kun for fair mønter der kun har to måder de kan lande. Hvad hvis vi vil vide hvad chancen for at få mindst 1 sekser når man slår 7 terninger er?
Så har vi en formel der ligner den fra før, men som er lidt længere, og som har det lange navn BINOMIALDISTRIBUTIONEN. Den ser sådan her ud: \[P(n,k,p)=\binom{n}{k} (p)^k (1-p)^{n-k}\] hvor det nye tal \(p\) er chancen for at slå f.eks. en sekser med en terning.
For en normal terning vil \(p=1/6 \), og så bliver \(p-1=5/6 \).
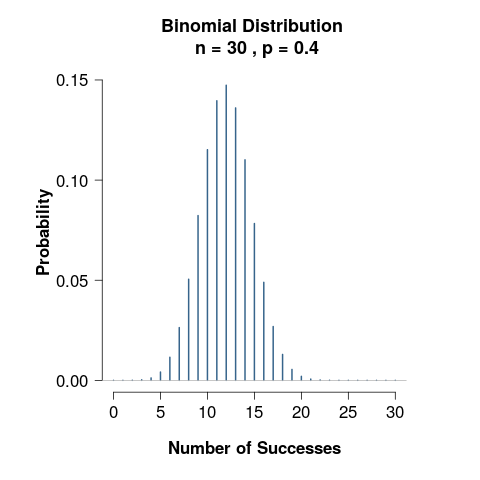
Her kan du se et plot over distributionen når \(n=30, p=0.4\) og \(k\) er ud af x-aksen.
Der er meget at tykke på på een gang, så lad os prøve den stille og roligt: Hvad er chancen for at slå præcis 1 seksere når man kaster 4 terninger?